Understanding the concepts of distance and displacement is essential for students of physics, engineering, and mathematics. These two terms appear similar and are often used interchangeably in everyday language, but in science, they carry very specific meanings.
Confusing the two can lead to wrong calculations, incorrect interpretations, and poor conceptual understanding.
In this detailed guide, we will explore what distance and displacement mean, how they differ, and why the distinction matters. We’ll break down the concepts using simple examples, formulas, and real-life applications so learners of all levels can fully grasp them.
Table of Contents
Introduction
Motion is one of the most fundamental topics in physics. Whether a car is driving along a road, a person is walking in a park, or a ball is thrown across a field, every motion involves a change in an object’s position over time.
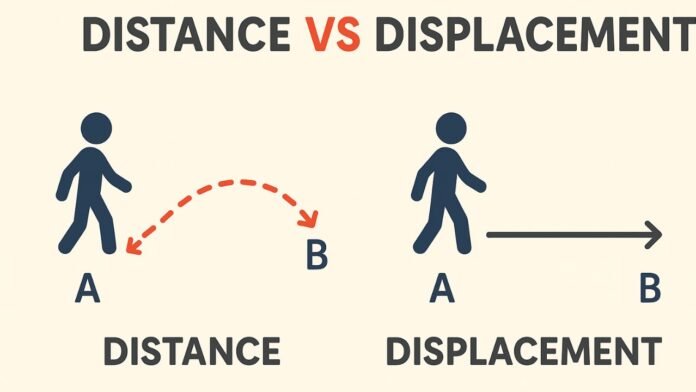
To measure how far something has moved, scientists use two key terms: distance and displacement. Both terms describe “how much an object has moved,” but the way they are measured and interpreted is completely different.
Distance is a scalar quantity, while displacement is a vector quantity. This distinction alone creates a major conceptual difference, but there is much more to unpack.
What Is Distance?
Distance is defined as the total length of the path traveled by an object, regardless of direction. It tells us how much ground has been covered.
Key Characteristics of Distance
- Scalar quantity (only magnitude, no direction).
- Always positive or zero.
- Depends on the actual path taken.
- Can never decrease during motion.
- Measured in meters (m) in the SI system.
Simple Example
Imagine you walk from point A to B following a curved path that covers 500 meters.
Even if the direct distance between A and B is only 300 meters, your distance traveled is still 500 meters, because distance considers the actual route you walked.
Real-Life Examples of Distance
- The kilometers shown on your car’s odometer.
- Steps counted on your fitness tracker.
- The total length of a hiking trail.
Distance is straightforward because it is simply the length of the path traveled—nothing more, nothing less.
What Is Displacement?
Displacement is defined as the shortest straight-line distance between the initial and final positions of an object, along with its direction.
Key Characteristics of Displacement
- Vector quantity (has both magnitude and direction).
- Can be positive, negative, or zero.
- Depends only on the initial and final positions, not the path.
- Can increase or decrease during motion.
- Measured in meters (m).
Simple Example
If you walk from A to B in a zigzag manner covering 500 meters, but the straight-line distance between A and B is 300 meters, then:
- Distance = 500 meters
- Displacement = 300 meters (in the direction from A to B)
Real-Life Examples of Displacement
- A drone flies 5 km north from its starting point. Its displacement is 5 km north.
- A bowler releases a ball, and it hits the pins. The displacement is the straight-line distance between the release point and the pins.
Unlike distance, displacement tells us how far you are from where you started, and in what direction.
The Fundamental Differences Between Distance and Displacement
The table below summarizes the differences clearly:
| Feature | Distance | Displacement |
| Type | Scalar | Vector |
| Direction | No | Yes |
| Path | Considers actual path | Only initial & final position |
| Value | Never negative | Can be zero, positive, negative |
| Symbol | d or s | Δx, Δs |
| Dependency | Path-dependent | Path-independent |
| Example | 10 km run with curves = 10 km | If you end at starting point = 0 displacement |
This table alone clarifies why the two terms should never be used interchangeably in physics.
How Distance and Displacement Are Calculated
Distance Formula
There is no single formula for distance because it depends on the actual path. However, in straight-line motion:
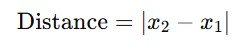
In curved motion, distance is the sum of the lengths of all segments.
Displacement Formula
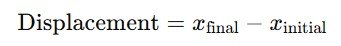
If motion occurs in two or three dimensions, displacement is calculated using the Pythagorean theorem:
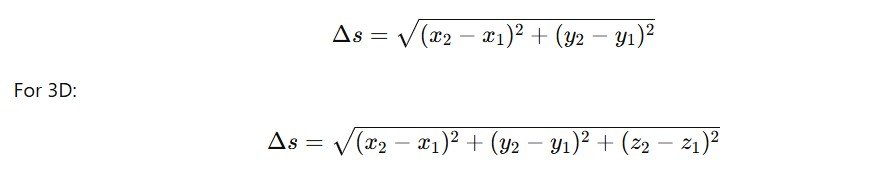
Understanding Through Practical Examples
Example 1: Walking Around a Park
You start at point A, walk around a circular park, and return to point A.
- Distance traveled: full circumference (say 400 m).
- Displacement: 0 m.
Because you end exactly where you started, your net change in position is zero.
Example 2: Driving From Home to School
Suppose your home and school are 5 km apart in a straight line. But the road curves, making the total driving distance 7 km.
- Distance: 7 km
- Displacement: 5 km (towards school)
Even though you drove more, your displacement is simply the straight-line measurement.
Example 3: Throwing a Ball Upward
You throw a ball straight up. It rises 20 meters and comes back into your hand.
- Distance = 20 m up + 20 m down = 40 m
- Displacement = 0 m (because it returns to the starting point)
Example 4: Movement in Two Dimensions
A person walks 3 m east, then 4 m north.
- Distance = 3 + 4 = 7 m
- Displacement = 5 m (northeast direction)
Using Pythagoras:
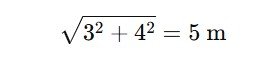
Graphical Interpretation
In motion graphs (position-time graphs):
- Distance corresponds to the total change in position regardless of direction.
- Displacement corresponds to the net change from the starting to the ending position.
Graph analysis helps students visually understand how displacement can be zero even when distance increases continuously.
Why Is the Difference Important?
Understanding distance and displacement is crucial because:
1. They affect calculations in kinematics
Speed uses distance, while velocity uses displacement:

This difference explains why your car’s speedometer shows speed, not velocity.
2. They determine physical interpretations
In physics, direction matters. Forces, velocities, and accelerations are vectors, so using displacement is essential.
3. They impact engineering and navigation
Pilots, sailors, and GPS systems rely on displacement to navigate efficiently.
4. They avoid conceptual errors
A misunderstanding here can lead to wrong answers in exams and problem-solving.
Real-World Applications
Sports
- A 400 m track race involves distance (400 m).
- But the displacement from start to finish is 0 m because the athlete completes a loop.
Navigation & GPS
GPS uses displacement (straight paths) to calculate “as-the-crow-flies” distance.
Robotics
Robots calculate displacement to determine the final location for positioning tasks.
Physics Experiments
In projectile motion, displacement determines range and trajectory.
Common Misconceptions
Misconception 1: Distance and Displacement are the same
This is only true when motion is in a straight line without changing direction.
Misconception 2: Displacement cannot be zero
Displacement can be zero if you return to your starting point.
Misconception 3: Displacement is always shorter
Displacement is always the shortest path, but in rare cases, such as perfectly straight-line motion, distance and displacement can be equal.
Distance vs Displacement in One Line
- Distance tells you how much you moved.
- Displacement tells you how far you are from where you started, and in which direction.
Conclusion
Distance and displacement may seem like simple concepts, but they form the foundation of understanding motion in physics.
Distance measures the complete path traveled, while displacement focuses only on the net change in position and direction. This distinction affects calculations of speed, velocity, and acceleration, making it essential for students, engineers, and anyone working with motion.
By grasping these concepts, learners not only strengthen their physics fundamentals but also improve their ability to solve real-world problems—from interpreting GPS routes to analyzing the trajectory of moving objects.
If you found this explanation helpful and need more blog articles on physics or any other subject, feel free to ask!